Compte-rendu de l’exercice sur le nucléaire japonais

Il y a quelques semaines, j’ai conçu un petit problème de physique nucléaire à l’intention des élèves du lycée Blaise Diagne de Dakar qui préparent le Bac scientifique prévu le 04 juillet prochain. En effet, dans le programme de physique des classes Terminale S au Sénégal, il existe un chapitre intitulé ‘’réactions nucléaires’’ qui s’intéresse à la radioactivité et à l’énergie atomique. L’exercice était donc à la portée des candidats même si certains ont jugé ‘’un peu compliquées’’ certaines questions. Voici, donc, la solution, détaillée au maximum afin de permettre à des journalistes comme Ziad Maalouf de Rfi et à tous les lecteurs profanes en la matière d’y comprendre quelque chose. Mais d’abord, quelques éléments pour comprendre ‘’l’essence des choses’’ comme disait Rabelais.

Le noyau d’un atome est globalement composé de protons et de neutrons qui forment un ensemble appelé nucléons. La masse atomique correspond au nombre de nucléons du noyau. En physique nucléaire, 2 atomes sont dits isotopes s’ils ont même nombre de protons. Ce qui les différencie, c’est donc le nombre de neutrons. Conclusion : Deux isotopes ont forcément des masses atomiques différentes. C’est pourquoi on symbolise un isotope par l’élément de l’atome complété par la masse atomique en haut à gauche. Les isotopes les plus connus du grand public sont le Carbone 12 et le carbone 14 (¹²C et ¹⁴C) ou encore l’Uranium 238 et l’uranium 235 (²³⁸U et ²³⁵U). Et c’est l’uranium 235 qui est utilisé dans les industries nucléaires.

L’uranium que l’on trouve à l’état naturel dans l’environnement est composé à plus de 99% de l’isotope 238. Il contient moins d’1% d’uranium 235. Or, il faut disposer d’un uranium qui contient au moins 5% d’isotope 235 pour l’utilisation dans les centrales nucléaires (nucléaire civil). Pour se faire, de grandes entités industrielles comme AREVA enrichissent l’uranium naturel, en augmentant la proportion en isotope 235 par divers procédés. L’enrichissement peut être léger (5%), faible (inférieur à 20%) ou fort (plus de 20%). Toutefois, la réglementation de l’Agence Internationale de Énergie Atomique (AIEA) fixe la limite à 20 % pour éviter l’usage militaire du nucléaire avec de l’uranium hautement enrichi. Mais, on le sait, il y a souvent un déphasage entre la loi et le respect de loi. Les iraniens ne vont certainement pas contredire mes dires.

Revenons maintenant à l’exercice

1. a) Pour faire simple, disons qu’en radioactivité, la demi-vie, encore appelée période radioactive, désigne le temps au bout duquel la moitié des atomes d’une source radioactive se désintègrent naturellement. Certains isotopes comme l’Iode 131 ont une demi vie relativement courte (à peine 8 jours) et d’autres peuvent aller jusqu’à des milliers, voire des millions d’années.

b) La fission nucléaire c’est, comme son nom l’indique, la fission d’un noyau lourd (comme l’uranium 235) en d’autres noyaux plus légers (qui constituent les déchets). Il s’agit de faire heurter un neutron sur un noyau d’uranium 235 qui se sépare ensuite en d’autres noyaux. Ces derniers sont, à leur tour, heurtés par d’autres 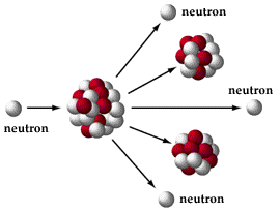neutrons libérés par le réaction précédente. C’est pourquoi on parle de réaction en chaine. Elle s’accompagne d’une importante quantité d’énergie qui peut être calculée à partir la formule E= MC² du plus grand physicien de tous les temps, Albert Einstein. Un petit schéma ci-contre en guise d’illustration.

La fusion, par contre, met en jeu deux noyaux légers qui fusionnent pour donner un noyau plus lourd. Elle se produit à température extrêmement élevée.

La différence fondamentale se situe au niveau des déchets. La première en produit beaucoup et reste le principal problème des pays nucléarisés alors que la seconde n’en produit pas. Le hic, c’est que les scientifiques n’arrivent pas encore à substituer la fission à la fusion dans les centrales atomiques pour produire du courant électrique. Ceci malgré les travaux de recherche et les projets comme Iter à Cadarache, en France.

Le deutérium et le tritium sont deux isotopes de l’atome d’hydrogène. La réaction de fusion entre ces deux éléments se passe au cœur du Soleil et abouti à la formation de l’Hélium. L’équation est

1. a). Le nombre N de fissions par seconde dans le réacteur n° 6 se calcul en partant du rendement R = 30% = 0,3.

On a R= Puissance électrique fournie/Puissance totale. Ici la puissance totale correspond à l’énergie dégagée par la réaction en 1 second qui est E= N x E’ avec E’ = 200Mev, l’énergie dégagée par 1 seul atome. On remarque que le nombre de fissions n’est rien d’autre que le nombre d’atomes.

Ainsi, on a 0,3 = 900.10⁶ / N x 200 x 1,6.10^-13 . Finalement, on tire N et on effectue le calcule. On trouve N = 9,375.10¹⁹ fissions.

Remarque : on convertit les Mégawatts en Watts en multipliant par 10⁶ et les Méga électronvolts (Mev) en joules en multipliant par 1,6.10^-13

b). Pour la masse d’uranium, on peut évaluer d’abord la masse d’uranium consommée en une seconde. Elle se calcule en multipliant le nombre N d’atomes par seconde par la masse atomique et par 1u pour convertir en kilogramme m’= N x 235 x 1u.

Ensuite on calcule pour une année bissextile qui compte 366 jours donc 366 x 24 heures et finalement 366 x 24 x 3600 secondes. En fin de compte, la masse demandée est

m = 9,375.10¹⁹ x 235 x 1,6605.10^-27 x 366 x 24 x 3600. On trouve m = 1 156 kilogrammes qui correspondent à m = 1,156 tonne.

1. a) L’équation de désintégration du Césium 137 s’écrit :
   

b) Pour trouver l’année à laquelle les alentours de la centrale seront épargnés par les radiations du Césium, on peut commencer par calculer la demi-vie de l’isotope par la formule T= ln2/λ.

T = ln2/ 7,32.10^-10 . Le résultat sera donné en seconde. En convertissant en années on trouve T= 30 ans. Mais, comme précisé plus haut, 30 ans c’est la demi-vie. Pour que les atomes se désintègrent entièrement, il faut donc multiplier par 2 ce qui donne 60 ans. Et si nous partons de 2011, l’année cherchée sera alors 2011 + 60 ans ce qui nous fait 2071.

Bonne chance à tous les candidats

Par @rons3