1 + 2 + 3 + 4 + 5 + … = -1/12 : Réalité ou délire mathématique ?

Qui disait que les mathématiciens sont des gens anormaux par définition ? Ah ! Je me souviens. C’est Jean Pierre Goux, un ingénieur et chercheur en maths appliquées, lors de son passage sur RFI il y a quelques années. C’est une caricature, évidemment. Il a certainement voulu dire que les mathématiciens cherchent parfois à pousser les limites de notre compréhension, à tel point qu’ils contredisent le bon sens commun. Certains finissent par perdre la raison. Le journaliste scientifique Laurent Lemire nous en fait découvrir quelques uns dans son ouvrage Les savants fous.

Moi j’ai failli devenir un peu fou ce week-end quand j’ai découvert sur la chaîne Youtube Numberphile un résultat des plus étonnants. Il s’agit de la valeur de la somme 1 + 2 + 3 + 4 + 5 + 6 + 7 + … ainsi de suite, la somme de tous les nombres entiers quoi. A votre avis, quel est le résultat de ce calcul ?

Eh bien, pas besoin d’avoir le Bac pour répondre que c’est « l’infini ».  Logiquement, plus le nombre de terme augmente, plus la somme devient de plus en plus grande. Si on continue jusqu’à l’infini on trouve l’infini, c’est évidement. Et pourtant, les mathématiciens ont prouvé que cette gigantesque somme vaut -1/12. Quoi ? Un si petit nombre ?  Négatif de surcroit ?  Ce n’est pas sérieux ! C’est absurde !  C’est du délire ! Comment une somme infinie peut-elle donner un nombre fini ? Comment une somme de termes positifs peut-elle aboutir à un résultat négatif ? Il est clair qu’il s’agit là d’un parfait canular. Nonnn mon ami ! C’est du sérieux. Selon les mathématiciens, cette somme équivaut bien à -1/12.  J’ai passé tout mon week-end à chercher un  sens à tout cela. Et, quelques articles plus tard, j’ai trouvé que ce résultat, d’apparence absurde, est même utilisé en physique théorique, notamment en mécanique quantique. Incroyable !

Qu’en est-il des preuves ?

J’ai vu qu’il y a plusieurs  méthodes de calcul qui permettent de retrouver ce résultat. Et, ce ne sont pas des blagues de mathématiciens du genre  »démontrer que 1=2’’ alors qu’une division par zéro, est malicieusement dissimulée quelque part. Ce sont des calculs sérieux de haut niveau qui font appel aux séries numériques, plus précisément aux séries divergentes. Je les avais apprises en 2e année de fac mais j’ai presque tout oublié. Et puis, c’est très compliqué à expliquer. Je ne vais donc pas m’aventurer sur ce terrain. Mais, pour les descendants d’Einstein qui souhaitent approfondir la question, il faut revoir la méthode de sommation de Cesaro, la méthode d’Abel, la méthode de Ramanujan et la régularisation par la fonction Zeta.

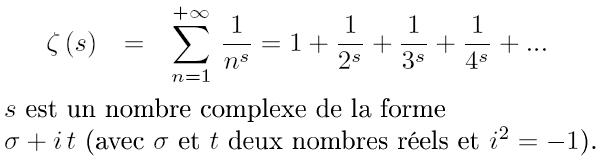
Et pour les autres, si vous avez fait les bancs jusqu’au collège au moins (niveau 4e), je peux vous expliquer la démonstration dont il est question dans la vidéo de Numberphile. Rassurez-vous, c’est hyper simple. Elle se fait en 3 étapes :

–

Considérons d’abord la somme
A= 1 – 1 + 1 – 1 + 1 – …

Vous pouvez aisément remarquer que le résultat de cette somme donne tantôt 0 tantôt 1.  Mais, il est possible de prouver qu’elle est égale à 1/2.

En effet, on peut voir que  A = 1 – 1 + 1 – 1 + 1 – … = 1– (1 – 1 + 1 – 1 + 1 – …). On remarque que le terme entre parenthèses n’est autre que A lui-même. Ainsi, on a : A = 1– A.

On résout l’équation pour tirer A. On obtient 2A = 1 d’où A = 1/2.

Considérons ensuite la somme
B = 1 – 2 + 3 – 4 + 5 – 6 + …

Même principe, on place une petite parenthèse et cela donne B = 1 – (2 – 3 + 4 – 5 + 6 – …). On décompose le terme entre parenthèse en deux entités et on obtient alors :

B = 1 – (1 – 2 + 3 – 4 + 5 – …) – (1 – 1 + 1 – 1 + 1 – …). On remarque ici dans la première parenthèse le terme B et dans la seconde le terme A. En remplaçant, on obtient :

B = 1 – B – A. Or A vaut 1/2. Donc B = 1 – B – ½, ce qui donne 2B = 1- ½ = ½ d’où B= ¼.

–

Considérons enfin notre gigantesque somme
S = 1 + 2 + 3 + 4 + 5 + 6 + …

On essaie de retrancher B de la somme S. On a :

 S – B = (1 + 2 + 3 + 4 + 5 + 6 + …) – (1 – 2 + 3 – 4 + 5 – 6 + …) Si on fait le calcul, on se rend compte que les nombres impairs s’annulent et les nombres pairs sont doublés. Ainsi, on a : S – B = 4 +  8 + 12 + … On factorise par 4 et on a :

S – B = 4 (1 + 2 + 3 + …)  et on retrouve la somme S entre parenthèses. Ce qui donne :

S – B = 4 S.  On résout l’équation pour tirer S :

On a 4S – S = -B  donc  3S  =  -B. Or, il on a déjà vu que B= ¼.  Donc 3S = -1/4 et finalement, S = – 1/12.  Et voilà ! CQFD.

Attention tout de même ! Cette preuve n’est pas si rigoureuse qu’elle n’en a l’air. Il n’y pas de problème apparent dans le raisonnement mais cette méthode de sommation n’est pas permise pour des sommes infinies. Cependant, elle permet de retrouver simplement notre résultat qui, je le rappelle, peut être prouvé de façon rigoureuse par les méthodes que j’ai évoqué plus haut.

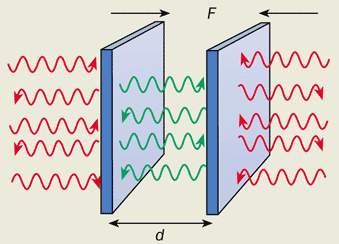
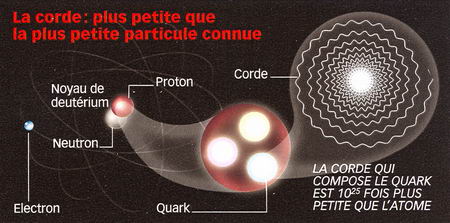
Je disais donc que ce résultat étonnant est utilisé en physique théorique. Il s’agit notamment de l’effet Casimir qui parle de la force d’attraction entre deux plaques parallèles conductrices placées dans le vide. Pour calculer cette force on utilise 1 + 2 + 3 + 4 + 5 + 6 + …= – 1/12.  Et cela marche puisqu’elle est prouvée expérimentalement. L’autre application de cette bizarrerie c’est dans la théorie des cordes avec l’explication de la dimension critique.

Cela ne vous étonne pas ? Moi je suis littéralement abasourdi.  Moi qui croyais que c’était si évident. Décidément ! « Évident est le mot le plus dangereux en mathématiques », comme disait Eric Temple Bell.